Επίλογος: Χάος, συμπεριφορά Hurst-Kolmogorov, και αβεβαιότητα
Έχετε ποτέ αναρωτηθεί πώς γίνονται οι προγνώσεις καιρού; Αν νομίζετε πως πρόκειται για μετεωρολόγους που κοιτούν δορυφορικές φωτογραφίες ή χάρτες καιρού και υποθέτουν πώς θα κινηθεί ο καιρός, κάνετε λάθος. Οι καιρικές προγνώσεις γίνονται με μοντέλα καιρού (αυτά είναι παρόμοια με τα κλιματικά μοντέλα, αλλά λειτουργούν σε διαφορετικές κλίμακες και έχουν μερικές άλλες διαφορές). Ας δούμε πώς γίνεται.
Κάθε 12 ώρες, μετεωρολογικές υπηρεσίες σε όλο τον κόσμο στέλνουν μετεωρολογικά μπαλόνια στην ατμόσφαιρα. Αυτά είναι μικρά αερόστατα που φέρουν κάμποσους μετεωρολογικούς αισθητήρες, όπως θερμόμετρο και βαρόμετρο, και ένα πομπό που εκπέμπει τις μετρήσεις σ' ένα σταθμό εδάφους. Καθώς το μπαλόνι ανεβαίνει, οι μετρήσεις εκπέμπονται, και έτσι καταγράφονται οι μετεωρολογικές μεταβλητές σε διάφορα υψόμετρα. Κατόπιν συλλέγονται αυτές οι μετρήσεις απ' όλο τον κόσμο, καθώς και μετρήσεις από πλοία και αεροπλάνα, και μας λένε πώς ήταν ο καιρός την ώρα των μετρήσεων. Για να γίνουν οι υπολογισμοί που απαιτούνται για την πρόγνωση, η ατμόσφαιρα διαιρείται σε μικρά τμήματα έτσι ώστε η θερμοκρασία, η πίεση, κλπ., σε κάθε τμήμα είναι γνωστή από τις μετρήσεις. Επειδή είναι γνωστοί οι φυσικοί νόμοι που περιγράφουν πώς οι συνθήκες σε κάθε τμήμα επηρεάζονται από τα γειτονικά του τμήματα, μπορούμε να υπολογίσουμε πώς θα εξελιχθούν οι συνθήκες σε κάθε τμήμα, και έτσι έχουμε πρόγνωση του καιρού. Το πλήθος των υπολογισμών είναι τεράστιο και μπορεί να πραγματοποιηθεί μόνο από υπολογιστή. Με άλλα λόγια, ο υπολογιστής προσομοιώνει την ατμόσφαιρα. Το σύστημα της προσομοίωσης ονομάζεται μοντέλο καιρού. Οι μεταβλητές εισόδου του μοντέλου (δηλαδή οι μετρήσεις του καιρού) λέγονται αρχικές συνθήκες.
Αυτός ο τρόπος πρόγνωσης πρωτοχρησιμοποιήθηκε στη δεκαετία του 1960. Ο Edward Lorenz, ένας από τους πρώτους επιστήμονες που πειραματίστηκε με μοντέλο καιρού, προσπάθησε να κάνει πρόγνωση δύο μηνών, και για κάποιο λόγο έκανε τους υπολογισμούς δυο φορές. Παρόλο που και τις δύο φορές χρησιμοποίησε το ίδιο μοντέλο και τις ίδιες αρχικές συνθήκες, τα αποτελέσματα ήταν εντελώς διαφορετικά. Αρχικά νόμισε πως είχε κάνει λάθος, αλλά αφού το διερεύνησε βρήκε ότι τη μία φορά είχε τρέξει την προσομοίωση στρογγυλεύοντας τις αρχικές συνθήκες στο έκτο δεκαδικό ψηφίο, ενώ την άλλη τις είχε στρογγυλεύσει στο τρίτο δεκαδικό ψηφίο [1]. Αυτό σημαίνει πως ακόμα κι αν μπορούσαμε να γνωρίζουμε επακριβώς τις αρχικές συνθήκες σε κάθε σημείο της γης (και της ατμόσφαιρας), και πάλι δεν θα μπορούσαμε να προγνώσουμε τον καιρό σε δύο μήνες, γιατί μια αρχική θερμοκρασία 31.23856 και μια αρχική θερμοκρασία 31.23857 θα έδιναν εντελώς διαφορετικά αποτελέσματα. Ο μαθηματικός όρος γι' αυτό είναι χάος: λέμε πως ένα σύστημα είναι χαοτικό αν απειροστές διαφορές στις αρχικές συνθήκες προκαλούν μεγάλες διαφορές στην κατάσταση του συστήματος μετά από κάποιο χρονικό διάστημα. Τα μοντέλα καιρού είναι χαοτικά, που σημαίνει πως γίνονται ασταθή όταν προσπαθούμε να προγνώσουμε τον καιρό για δύο μήνες μετά.
Ένας άλλος τρόπος να το εξηγήσουμε είναι το γνωστό παράδειγμα με τον τυφώνα και την πεταλούδα. Αν προσπαθούσαμε να προγνώσουμε αν θα δημιουργηθεί τυφώνας στην Αμερική σε ένα μήνα, και γνωρίζαμε ακριβώς τους φυσικούς νόμους που περιγράφουν τη δημιουργία του τυφώνα, και γνωρίζαμε τις αρχικές συνθήκες (τις τωρινές συνθήκες) σε κάθε σημείο της ατμόσφαιρας, και πάλι δεν θα μπορούσαμε να κάνουμε πρόγνωση· γιατί ακόμα και μια πεταλούδα που θα κουνούσε τα φτερά της στην Κίνα θα αλλοίωνε τις συνθήκες αρκετά έτσι ώστε το αποτέλεσμα να είναι εντελώς διαφορετικό. Αυτό δεν σημαίνει πως η πεταλούδα είναι το αίτιο του τυφώνα· σημαίνει πως η δημιουργία του τυφώνα είναι τόσο ευαίσθητη στις απειροστές διαφορές που μπορεί να υπάρχουν στα «αίτια» ώστε τελικά η σχέση αιτίου-αιτιατού πρακτικά εξαφανίζεται και ο τυφώνας ανάγεται σε τυχαίο φαινόμενο.
Ίσως είναι πιο εύκολο στην κατανόηση αν αντί για τυφώνα προσπαθούμε να προβλέψουμε το αποτέλεσμα της ρουλέτας. Υποθέτουμε πως ξέρουμε ό,τι χρειάζεται για να υπολογίσουμε το αποτέλεσμα της ρουλέτας: την αρχική ταχύτητα της μπίλιας, την αρχική γωνιακή ταχύτητα του τροχού, το βάρος, την ελαστικότητα, και τις άλλες ιδιότητες της μπίλιας, τις ιδιότητες του τροχού, τη θερμοκρασία της μπίλιας, του τροχού και της ρουλέτας, τη θερμοκρασία, πίεση, και υγρασία του αέρα, κλπ. Θα μπορούσαμε να προβλέψουμε το αποτέλεσμα; Η απάντηση είναι όχι, γιατί και αυτό είναι χαοτικό, με την προϋπόθεση να δώσουμε αρκετά μεγάλη αρχική ταχύτητα στη μπίλια και στον τροχό. Μια τυχαία σύγκρουση ενός μορίου αέρα θα μπορούσε να δημιουργήσει αρκετή διαφορά για να αλλάξει το αποτέλεσμα. Αυτό δεν σημαίνει πως η σύγκρουση είναι η αιτία του αποτελέσματος· το αποτέλεσμα εξαρτάται ταυτόχρονα από τα πάντα και από τίποτε, τελικά δηλαδή είναι τυχαίο.
Η ρουλέτα είναι τεχνητό σύστημα με μόνο 37 δυνατά αποτελέσματα, καθένα με ίση πιθανότητα. Τα φυσικά συστήματα είναι πολύ πιο σύνθετα. Η ατμόσφαιρα είναι εξαιρετικά πιο περίπλοκη, και ενώ τα μοντέλα καιρού μπορούν να προβλέψουν τον καιρό για τρεις, καμιά φορά και για τέσσερις ή πέντε μέρες, δεν μπορούν να κάνουν κάτι καλύτερο, και όσο κι αν βελτιωθούν τα μοντέλα ή η ακρίβεια με την οποία γνωρίζουμε τις αρχικές συνθήκες, ποτέ δεν θα μπορούμε να προγνώσουμε για περισσότερο από δύο εβδομάδες, γιατί δεν ξέρουμε τι κάνουν ή τι θα κάνουν όλες οι πεταλούδες του κόσμου, πόσο μάλλον όλα τα μόρια της ατμόσφαιρας.
Υπάρχουν, όμως, σημαντικά πράγματα που γνωρίζουμε για τη ρουλέτα. Παρόλο που τα αποτελέσματά της είναι τυχαία, ξέρουμε πως η μέση τιμή είναι 18, και πως η τιμή κυμαίνεται με ομοιόμορφο τρόπο από 0 ως 36. Μπορούμε να φανταστούμε τα αποτελέσματα της ρουλέτας σαν τυχαίες διακυμάνσεις γύρω από μια μέση τιμή 18, όπως δείχνει το Σχήμα 1. Όμως η ρουλέτα είναι ένα εξαιρετικά απλό τεχνητό σύστημα. Τα φυσικά συστήματα είναι πολύ πιο σύνθετα.
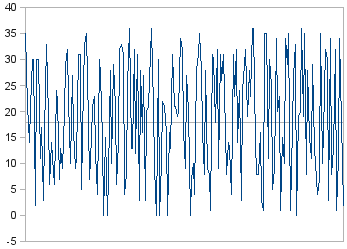
Σχήμα 1: 200 τυχαία αποτελέσματα ρουλέτας
Πολλοί άνθρωποι σκέφτονται για το κλίμα με περίπου τον ίδιο τρόπο που σκέφτονται για τη ρουλέτα, και αυτή είναι η κυρίαρχη άποψη στην επιστήμη του κλίματος. Θεωρείται πως το «κλίμα», ή «σήμα», είναι κάτι σαν τη μέση τιμή της ρουλέτας, και πως ο «καιρός», ή «θόρυβος», είναι κάτι σαν μια μεμονωμένη έκβαση της ρουλέτας. Εικάζεται πως η μέση θερμοκρασία της γης είναι, ας πούμε, 15°C, αλλά η θερμοκρασία στην Αθήνα στις 13 Απριλίου 2009 μπορεί να είναι 22°C, όπως ακριβώς η μέση τιμή της ρουλέτας είναι 18 αλλά μια μεμονωμένη έκβαση μπορεί να είναι 31. Αν εξαγάγουμε τη μέση τιμή πολλών αποτελεσμάτων ρουλέτας, το αποτέλεσμα θα είναι 18· και υποτίθεται πως, αντίστοιχα, αν εξαγάγουμε τη μέση τιμή της θερμοκρασίας σε όλα τα σημεία της γης για πολλά διαδοχικά χρόνια, το αποτέλεσμα θα είναι π.χ. 15°C. Τα αποτελέσματα της ρουλέτας διαφέρουν, αλλά η μέση τιμή τους παραμένει ίδια. Αν η μέση τιμή της ρουλέτας μεταβληθεί, θα υπάρχει συγκεκριμένος λόγος γι' αυτό, όπως τροποποίηση του τροχού· και γίνεται αντίστοιχα η παραδοχή πως μια αλλαγή στο «υποκείμενο κλίμα» θα έχει πάντα συγκεκριμένη αιτία.
Εντούτοις, όπως βλέπουμε στο Σχήμα 2, που δείχνει τη θερμοκρασία κατά τα τελευταία 10 χιλιάδες χρόνια, η μακροπρόθεσμη συμπεριφορά της θερμοκρασίας δεν μοιάζει καθόλου με της ρουλέτας· και αν το εξετάσουμε σε κλίμακα 100 χιλιάδων ετών (Σχήμα 3) ή 800 χιλιάδων ετών (Σχήμα 4), θα δούμε πως όχι μόνο η κατάσταση δεν βελτιώνεται, αλλά και πως αυτό που βλέπουμε κάθε φορά δεν μοιάζει καθόλου με ό,τι θα είχαμε υποθέσει από το προηγούμενο διάγραμμα. Είναι πιθανό πως αν είχαμε δεδομένα για ακόμα παλιότερα, και μπορούσαμε να το δούμε σε κλίμακα ακόμα μεγαλύτερη, και πάλι η εικόνα θα ήταν πολύ διαφορετική απ' ό,τι περιμένουμε κοιτάζοντας το Σχήμα 4. Αυτό που μοιάζει με «σήμα» στο Σχήμα 2 είναι «θόρυβος» στο Σχήμα 3, και αυτό που μοιάζει με «σήμα» στο Σχήμα 4 θα φαινόταν σαν «θόρυβος» αν είχαμε δεδομένα για να μεγαλώσουμε περαιτέρω την κλίμακα.
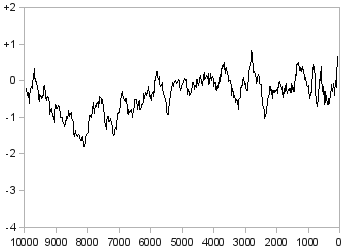
Σχήμα 2: Η θερμοκρασία της γης τα τελευταία 10 χιλιάδες χρόνια (διαφορά σε σχέση με σήμερα σε °C)
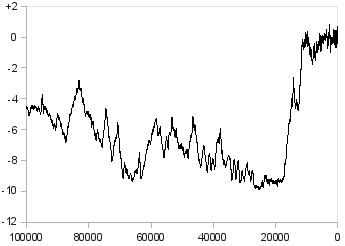
Σχήμα 3: Η θερμοκρασία της γης τα τελευταία 100 χιλιάδες χρόνια (διαφορά σε σχέση με σήμερα σε °C)
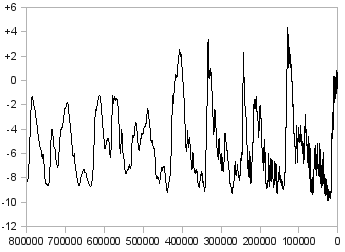
Σχήμα 4: Η θερμοκρασία της γης τα τελευταία 800 χιλιάδες χρόνια (διαφορά σε σχέση με σήμερα σε °C) [2]
Η ρουλέτα είναι απρόβλεπτη βραχυπρόθεσμα, αλλά προβλέψιμη μακροπρόθεσμα: μπορούμε να φανταζόμαστε τις διάφορες εκβάσεις σαν τυχαίο θόρυβο πάνω σ' ένα γνωστό σήμα. Η ρουλέτα έχει μεγάλη αβεβαιότητα σε μικρή κλίμακα, αλλά μεγάλη βεβαιότητα σε μεγάλη κλίμακα. Το κλίμα είναι το ίδιο αβέβαιο σε όλες τις κλίμακες. Στην πραγματικότητα, μαθηματική ανάλυση του κλίματος δείχνει πως η συμπεριφορά του είναι τέτοια ώστε η αβεβαιότητα να είναι η μέγιστη δυνατή σε όλες τις κλίμακες. Αυτή η μεγιστοποίηση της αβεβαιότητας σε όλες τις κλίμακες λέγεται συμπεριφορά Hurst-Kolmogorov των κλιματικών διεργασιών [3].
Η φύση αγαπά την αβεβαιότητα, και μας ξεγελά με δύο τρόπους: από τη μια δεν θα μπορούσαμε να προβλέψουμε το μέλλον του κλίματος, ακόμα κι αν γνωρίζαμε πλήρως τους φυσικούς νόμους που το κυβερνούν, λόγω του χάους· και από την άλλη, δεν μπορούμε να είμαστε πολύ σίγουροι για τη στατιστικά αναμενόμενη συμπεριφορά του κλίματος που βασίζεται στις παρατηρήσεις του παρελθόντος, λόγω της συμπεριφοράς Hurst-Kolmogorov.
Οι αλλαγές στο κλίμα και στον καιρό άλλοτε έχουν μια δεσπόζουσα αιτία, και άλλοτε είναι χαοτικές. Οι εποχές, για παράδειγμα, οφείλονται στο γεγονός ότι οι ακτίνες του ήλιου πέφτουν υπό διαφορετική γωνία το καλοκαίρι και το χειμώνα. Μια καταιγίδα ή ένας καύσωνας συνήθως δεν έχουν δεσπόζουσα αιτία, αλλά δημιουργούνται χαοτικά. Γιατί αλλάζει το κλίμα; Και πάλι, μπορεί να υπάρχουν συγκεκριμένες δεσπόζουσες αιτίες, ή μπορεί η αλλαγή να είναι χαοτική. Η υπόθεση της ανθρωπογενούς κλιματικής αλλαγής λέει πως οι εκπομπές αερίων θερμοκηπίου από τις ανθρώπινες δραστηριότητες είναι η δεσπόζουσα αιτία· αλλά δείξαμε πως αυτή η υπόθεση είναι αβάσιμη. Αν υπάρχει κάποια άλλη δεσπόζουσα αιτία ή αν πρόκειται για συνηθισμένες χαοτικές αλλαγές δεν είναι ξεκαθαρισμένο. Νιώθουμε πως πρόκειται για το δεύτερο. Νιώθουμε πως η άγνοιά μας για τα αίτια της κλιματικής αλλαγής δεν οφείλεται στο ότι δεν έχουμε μετρήσει και μελετήσει αρκετά, αλλά στο ότι η αβεβαιότητα είναι δομημένη μέσα στο κλίμα, όπως είναι δομημένη στην ίδια τη ζωή. Οι άνθρωποι επηρεάζουν το κλίμα από τότε που υπάρχουν, όπως και οι πεταλούδες· και οι ενέργειές τους αλληλεπιδρούν με άπειρες άλλες ενέργειες και συμβάλλουν σε ένα απείρως πολύπλοκο και εντελώς απρόβλεπτο σύστημα, που εξαρτάται από τα πάντα αλλά και από τίποτε, που είναι ταυτόχρονα ντετερμινιστικό και τυχαίο.
Harold Hurst
(1880–1978)
|
Αντρέι Κολμογκόροφ
(1903–1987)
|
Αναφορές
| [1] | N. G. Cooper, From Cardinals to Chaos: Reflections on the life and legacy of Stanislaw Ulam, Cambridge Univ. Press, 1989. |
| [2] | J. Jouzel et al., EPICA Dome C Ice Core 800KYr Deuterium Data and Temperature Estimates, IGBP PAGES/World Data Center for Paleoclimatology, Data Contribution Series #2007-091, NOAA/NCDC Paleoclimatology Program, Boulder CO, USA; ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/epica_domec/edc3deuttemp2007.txt, accessed on 2009-08-06. |
| [3] | Για περισσότερα για τη συμπεριφορά Hurst-Kolmogorov, βλέπε τις σχετικές εργασίες του Κουτσογιάννη, κατάλογος των οποίων βρίσκεται στη διεύθυνση http://www.itia.ntua.gr/en/documents/?tags=Hurst (Νεότερα: [4]). Μια σχετικά εύκολη εισαγωγή είναι η εξής: D. Koutsoyiannis, Nonstationarity versus scaling in hydrology, Journal of Hydrology 324 (1-4), 239–254, doi: 10.1016/j.jhydrol.2005.09.022, 2006; available at http://www.itia.ntua.gr/en/docinfo/673/, accessed on 2009-08-03. Η σημασία των σχετικών εργασιών του Κολμογκόροφ και του Hurst είναι ιστορική: A. N. Kolmogorov, Wienersche Spiralen und einige andere interessante Kurven in Hilbertschen Raum, Doklady Akademii Nauk URSS 26, 115–118, 1940. H. E. Hurst, Long term storage capacities of reservoirs, Transactions of the American Society of Civil Engineers 116, 776–808, 1951. |
Νεότερα
| [4] | Για περισσότερες πληροφορίες για όλα τα θέματα με τα οποία καταπιάνεται αυτό το κεφάλαιο, συνιστούμε πλέον την εξαιρετική και διαφωτιστική νέα εργασία του Κουτσογιάννη: D. Koutsoyiannis, A random walk on water, Hydrology and Earth System Sciences 14, 585–601, 2010; available at http://itia.ntua.gr/el/docinfo/923/. 16 Απριλίου 2010 |

